geometria nei film
La bellezza delle inquadrature geometriche
Linee che dividono l'immagine o creano motivi ricorrenti o suddivisioni ordinate, in famose scene del cinema e della tv
Altri articoli su questo argomento
Cerchi nel cerchio [Pillole]
Niente matematica, stavolta: solo un bel disegno
![Cerchi nel cerchio [Pillole]](https://www.ilpost.it/wp-content/uploads/2019/10/ilpost-anteprima-colore.png)
Fullerene
Sabato scorso Google ha ricordato i venticinque anni della scoperta del fullerene modificando il suo logo. Ma quali sono le proprietà matematiche della struttura molecolare del fullerene?
Comitato per l’abolizione di pi greco
È vero, il valore di π è quello e non lo si può cambiare per legge (quantunque ci avessero tentato...). Però non è affatto detto che il rapporto tra circonferenza e raggio di un cerchio sia stata la scelta migliore per fissare la costante!
La piastrella di Kürschák
O di come calcolare l'area di un dodecagono inscritto in un cerchio di lato unitario.
Bandiere geometriche [Pillole]
La bandiera nepalese è davvero geometrica
Il crivello dopo Eratostene
Non è che ci siano chissà quali metodi per calcolare i numeri primi. Può essere divertente scoprire che esiste un crivello... geometrico.
Il teorema di Pitagora spiegato con l’acqua
In questi giorni è tornato a circolare un vecchio video che mostra in maniera molto ingegnosa perché a²+b²=c²
Geometrie non euclidee
Nel XIX secolo i matematici hanno avuto finalmente il coraggio di accettare l'idea che il postulato delle parallele non fosse necessariamente vero. Nacquero così altre due geometrie con assiomi diversi: quella ellittica e quella iperbolica.
Il teorema di Pitagora
Il teorema più famoso della geometria merita indubbiamente una trattazione a sé.
Gli assiomi dimenticati da Euclide
Dopo aver scoperto la geometria ellittica e quella iperbolica, i matematici hanno anche trovato dei loro modelli nello spazio euclideo, mostrando così come ness. Da lì si è giunti a scoprire come le fondazioni della geometria non erano poi così solide.
Il quinto postulato di Euclide
Quello delle geometrie non euclidee è un tema che non può mancare in un blog di divulgazione matematica; il difficile è riuscire a dire qualcosa di diverso dal solito. Cominciamo a vedere la storia dei tentativi di dimostrazione.
Il “cappello” a un annoso problema matematico
Sembra sia stato infine scoperto un "einstein", cioè una forma che può ricoprire una superficie infinita senza mai ripetere lo stesso motivo
Trisecare un angolo con riga, squadra e compasso
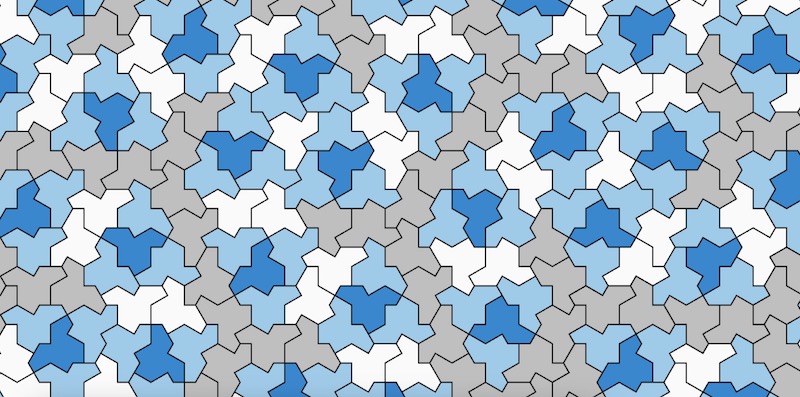
Il trucco c'è, e si vede...
Foto in bianco e nero dai Mondiali
La faccia di Oscar Tabarez, il sudore di Cristiano Ronaldo e l'architettura degli stadi, da guardare senza colori
Fabbriche di tessuti
Il fotografo americano Chris Payne ha visitato i luoghi in cui da decenni vengono lavorati e prodotti tessuti, i materiali con cui "siamo a contatto tutto il tempo"
Per la prima volta il premio Abel, uno dei più importanti riconoscimenti per i matematici, è stato assegnato a una donna
Lo ha vinto la matematica statunitense Karen Uhlenbeck
15 infografiche per capire meglio le bandiere di tutto il mondo
Quali sono i colori più utilizzati? E le forme? Perché sono così spesso formate da tre strisce verticali?
Il mondo è fatto di pattern
Album fotografico di linee e disegni che si ripetono in schemi geometrici e armoniosi: cespi di banane, piccoli cactus, risaie, e il mantello di una zebra
