Il teorema di Pitagora spiegato con l’acqua
In questi giorni è tornato a circolare un vecchio video che mostra in maniera molto ingegnosa perché a²+b²=c²

In questi giorni è tornato a circolare un vecchio video, caricato su YouTube per la prima volta nel 2009, che mostra in maniera molto efficace il teorema di Pitagora: cioè quello che dice che in un triangolo rettangolo i quadrati costruiti sui cateti (i due lati più corti) hanno sempre un’area uguale a quella del quadrato costruito sull’ipotenusa (il lato più lungo). Il teorema si esprime con l’equazione: a²+b²=c².
E qui la GIF, se volete fare i brillanti con i vostri amici.
https://twitter.com/Learn_Things/status/726840328624345088
Il teorema prende il nome dal matematico greco Pitagora, che visse tra il 570 e il 495 a.C. La sua formulazione era probabilmente già conosciuta a matematici e astronomi babilonesi, indiani e forse cinesi, ma le fonti antiche di solito attribuiscono a Pitagora la prima dimostrazione del teorema. La dimostrazione è solo “attribuita” a Pitagora perché nessun suo scritto originale è sopravvissuto fino ai giorni nostri. La dimostrazione di Pitagora è mostrata nell’immagine in basso.
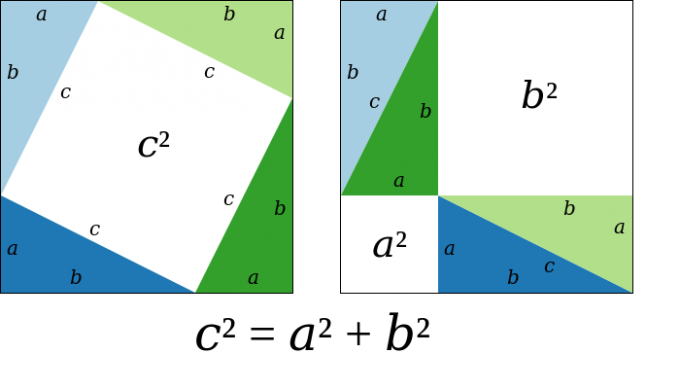
(William B. Faulk/WikiMedia)




