Il “cappello” a un annoso problema matematico
Sembra sia stato infine scoperto un "einstein", cioè una forma che può ricoprire una superficie infinita senza mai ripetere lo stesso motivo
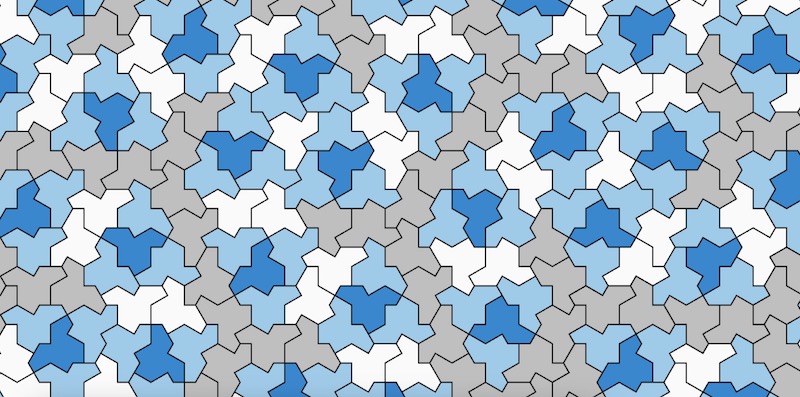
Sembra sia stato infine scoperto un "einstein", cioè una forma che può ricoprire una superficie infinita senza mai ripetere lo stesso motivo

Un concetto familiare a tutti diventa piuttosto sfuggente quando bisogna definirlo: una cannuccia, per esempio, quanti fori ha?
Alla fine ce ne possono stare più di quanto si possa pensare
![[Pillole] Tenere a distanza le persone](https://www.ilpost.it/wp-content/uploads/2019/10/ilpost-anteprima-colore.png)
Quello che fanno fare a scuola, tagliando una striscia di carta e poi unendone gli estremi dopo averne torto uno di 180 gradi

Un'app per fare geometria pratica.
![Pythagorea [Pillole]](https://www.ilpost.it/wp-content/uploads/2019/10/ilpost-anteprima-colore.png)
O di come calcolare l'area di un dodecagono inscritto in un cerchio di lato unitario.

Il trucco c'è, e si vede...

In questi giorni è tornato a circolare un vecchio video che mostra in maniera molto ingegnosa perché a²+b²=c²

Niente matematica, stavolta: solo un bel disegno
![Cerchi nel cerchio [Pillole]](https://www.ilpost.it/wp-content/uploads/2019/10/ilpost-anteprima-colore.png)
La bandiera nepalese è davvero geometrica
![Bandiere geometriche [Pillole]](https://www.ilpost.it/wp-content/uploads/2019/10/ilpost-anteprima-colore.png)
Zhang Bojun ha fotografato per sette anni folle di persone cinesi, e con le migliaia di foto raccolte ha costruito immagini fatte di motivi geometrici colorati

Perché la geometria non basta e ci vuole l'algebra (e non solo!)

Si chiama Maryam Mirzakhani ed è una scienziata iraniana: ha vinto il premio considerato l'equivalente del Nobel per la matematica

Punto, retta e piano sono davvero concetti così naturali da non poter essere diversi? Mica tanto.

Una galleria fotografica che mostra quando la realtà imita la geometria

Negli spazi multidimensionali le ipersfere sono sempre meno grandi... e così arriviamo a un paradosso.

Non è che ci siano chissà quali metodi per calcolare i numeri primi. Può essere divertente scoprire che esiste un crivello... geometrico.

È vero, il valore di π è quello e non lo si può cambiare per legge (quantunque ci avessero tentato...). Però non è affatto detto che il rapporto tra circonferenza e raggio di un cerchio sia stata la scelta migliore per fissare la costante!

Dopo aver scoperto la geometria ellittica e quella iperbolica, i matematici hanno anche trovato dei loro modelli nello spazio euclideo, mostrando così come ness. Da lì si è giunti a scoprire come le fondazioni della geometria non erano poi così solide.

Nel XIX secolo i matematici hanno avuto finalmente il coraggio di accettare l'idea che il postulato delle parallele non fosse necessariamente vero. Nacquero così altre due geometrie con assiomi diversi: quella ellittica e quella iperbolica.
