Come sette ponti portarono a una nuova matematica
Cominciò tutto a Königsberg quasi tre secoli fa con un problema irrisolvibile, che stimolò l'immaginazione di Eulero
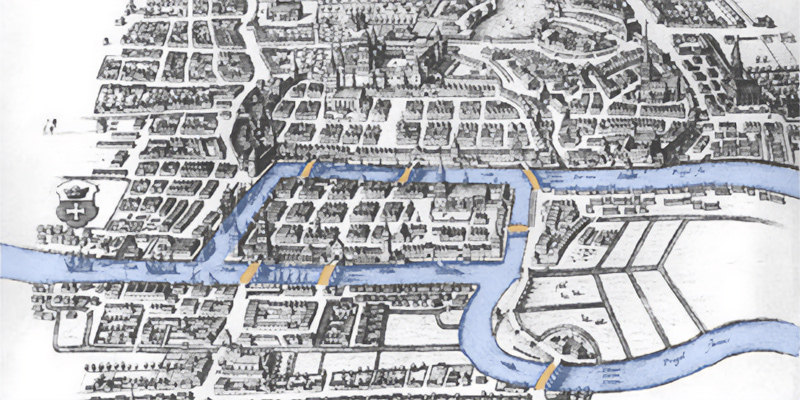
Cominciò tutto a Königsberg quasi tre secoli fa con un problema irrisolvibile, che stimolò l'immaginazione di Eulero

Una volta che si cambia punto di vista, si possono avere idee che portano a nuovi sviluppi... basta sapere accorgersi di cosa bisogna buttare via. Anche questo è il bello dela matematica.

Con un mesetto di ritardo, mi dedico anch'io al debunking matematico

Le sue formule e teorie sono ricordate nel doodle di Google di oggi, per il 306esimo anniversario della sua nascita

Il suo contributo non sarà forse stato "profondo", ma sicuramente ha avuto un'enorme influenza.

La scoperta di oggi: è possibile scoprire il numero di dèi dell'universo studiando la topologia dell'universo!

A differenza di pi greco, è più semplice da trattare, almeno da un punto di vista elementare [Continua]

Il fatto che oggi sia il compleanno di Leonardo da Vinci e di Eulero non significa poi molto.

Leggendo questo libro darete un nuovo significato alla frase "la musica e la matematica hanno molto in comune"

Da un banale gioco a testa o croce non solo si può arrivare a una vincita potenzialmente infinita, ma addirittura la vincita media è infinita!

Ma la "non-notizia" merita comunque qualche riga [Continua]

Non è che ci siano chissà quali metodi per calcolare i numeri primi. Può essere divertente scoprire che esiste un crivello... geometrico.

In generale possiamo accettare senza troppi problemi che le nozioni e i concetti matematici siano veri. Ma questo non significa necessariamente che siano reali. Peccato che neppure i matematici siano d'accordo sulla realtà della matematica.

La storia del sudoku è istruttiva: un gioco può affiorare in superficie in tempi e luoghi diversi, ma il successo arriverà per caso.

Il concetto di infinito in matematica è sempre stato trattato con le molle, già dai greci; non ci si sentiva a proprio agio con i paradossi relativi, e il grande traguardo degli analisti del XIX secolo fu di eliminarlo. Poi però...

Molte successioni hanno una somma infinita, altre hanno una somma finita. La serie armonica va sì all'infinito, ma così piano che uno magari non se ne accorge nemmeno.

Per decenni è stata alla base di molte politiche economiche, per prevedere come le persone gestiscono un guadagno inatteso: ma forse il grande economista si sbagliava

La congettura di Goldbach resiste da quasi tre secoli ai tentativi di dimostrazione. Ci è voluta una Fields Medal per ottenere un nuovo risultato dopo ottant'anni.

Negli ultimi cinquant'anni si è verificato un allontanamento tra i matematici e i fisici; sempre più matematici sono convinti di poter fare a meno della fisica, mentre altri ritengono che fare matematica per sé stessa la faccia diventare un esercizio sterile. Cosa c'è di vero in tutto questo?
