No, l’Ipotesi di Riemann non è ancora stata risolta

Non so se qualcuno sia saltato sulla sedia leggendo questo lancio Ansa. L’Ipotesi di Riemann è il sacro Graal della matematica: quando ero studente universitario correva voce che ci fosse qualcuno che aveva pronto un manoscritto che presentava tutti i risultati che si potevano ricavare se la congettura fosse stata dimostrata. Ok, potete rimettervi a sedere: la congettura non è stata dimostrata. Ma la “non-notizia” merita comunque qualche riga.

Per prima cosa, provo a spiegare cos’è l’Ipotesi di Riemann (RH nel seguito, dal termine inglese “Riemann Hypothesis”) e perché è così importante. È noto sin dal Medioevo che la somma degli inversi dei numeri naturali cresce fino all’infinito, anche se con molta calma. La somma degli inversi dei quadrati dei numeri naturali invece ha un valore finito, che Eulero con un po’ di magheggi dimostrò essere π²/6. Nel 1859, il grande matematico tedesco Bernhard Riemann cominciò a prendere la somma degli inversi dei numeri naturali elevati a una potenza qualunque, e generalizzò questa funzione – che in suo onore si chiama la zeta di Riemann – usando potenze che sono numeri complessi. Riemann dimostrò che la sua funzione ζ(s) assumeva il valore zero quando s era un numero negativo pari e per un numero infinito di valori complessi la cui parte reale è compresa tra 0 e 1. Gli sembrava però che quei valori stessero tutti su una retta, quella per cui la parte reale vale esattamente 1/2. Se fosse davvero così, si potrebbe dimostrare che la successione dei numeri primi è sì casuale, ma in un certo senso il meno casuale possibile; in altre parole, la formula li(n) – si legge “logaritmo integrale di n” – che approssima la quantità di numeri primi minori di un qualunque n commette un errore “limitato”. (L’errore c’è, proprio perché i numeri primi si sparpagliano in modo apparentemente strano.) Peccato che in un secolo e mezzo nessuno sia riuscito a dimostrare che gli zeri stanno davvero tutti su quella retta!

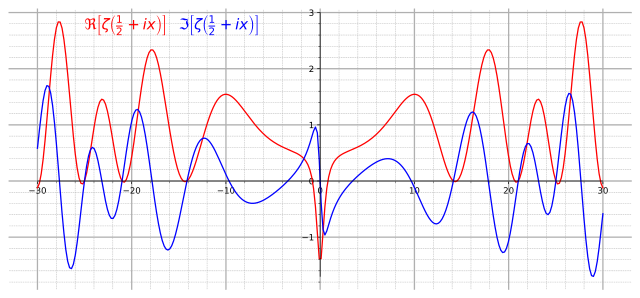
Ok. Come si è arrivati a questo lancio di agenzia? Semplice. I fisici Giuseppe Mussardo e André LeClair hanno pubblicato un articolo in cui, usando per l’appunto metodi di tipo fisico e non matematico, hanno dimostrato (matematicamente!) che “while a violation of the RH is strictly speaking not impossible, it is however extremely improbable.”; tradotto in italiano, è tecnicamente possibile che RH sia falsa, ma la cosa è estremamente improbabile. La Sissa – dove lavora Mussardo – ha pubblicato un comunicato stampa dal titolo “La congettura di Riemann svelata dalla fisica”. Notate come non ci sia scritto “dimostrata” ma “svelata”: termine tecnicamente corretto per l’articolo ma ambiguo. Infine l’Ansa ha preso il comunicato stampa e invece che “svelata” ha usato “risolta”, facendo così saltare sulla sedia la gente che l’ha letto. Un tipico esempio di telefono senza fili, insomma: la notizia originale si trasforma tra un passaggio e l’altro.

Quello che può essere interessante è notare la differenza di approccio tra i fisici e i matematici. Questi ultimi vogliono che una dimostrazione accerti le cose senza ombre di dubbio; i primi sono più interessati a un comportamento generico della funzione, e quindi accettano risultati probabilistici. Si può capire la cautela dei matematici: se andate qui e guardate la differenza tra li(n) e π(n), cioè il numero di primi minori di n, vedete che al crescere di n questa differenza continua a crescere, e si potrebbe immaginare – lo ha fatto anche Gauss, mica albicocche artiche! – che continuerà ad andare avanti così. E invece un centinaio di anni fa Littlewood ha dimostrato che la differenza passerà da positiva a negativa infinite volte. Ma non è così facile accorgersene, visto che π(n) diventa per la prima volta maggiore di li(n) quando n vale più o meno 10³¹⁶…

Detto questo, però, non intendo sminuire l’approccio di Mussardo e LeClair, e questo per due ragioni. La prima è che, almeno per me, è incredibile pensare come qualcosa di assolutamente asettico ed etereo come la distribuzione dei numeri primi possa avere un significato fisico. La seconda è che in effetti esistono “dimostrazioni probabilistiche” in matematica! Se leggete la voce relativa, scoprirete come. Quindi è vero che l’ipotesi di Riemann non è ancora stata dimostrata, ma è possibile che prima o poi una strada come quella porti alla soluzione…

Aggiornamento: il lancio Ansa è stato eliminato, ma per i curiosi ne è rimasta copia.