Numeri altamente composti
Basta con le divisioni che non terminano mai! O almeno cerchiamo di ridurle al minimo indispensabile. E come? Con i numeri altamente composti...

Basta con le divisioni che non terminano mai! O almeno cerchiamo di ridurle al minimo indispensabile. E come? Con i numeri altamente composti...

Il 14 di Cruijff, Maradona che rischiò di giocare con il 12, Gatti che scelse il 44 (sì, per quello) e Zamorano che sfruttò le addizioni

una categoria di numeri con proprietà facili da studiare... ma non troppo.

Il governo italiano se l'è presa per come sono stati interpretati, e ha risposto all'agenzia Frontex giocando un po' con i numeri
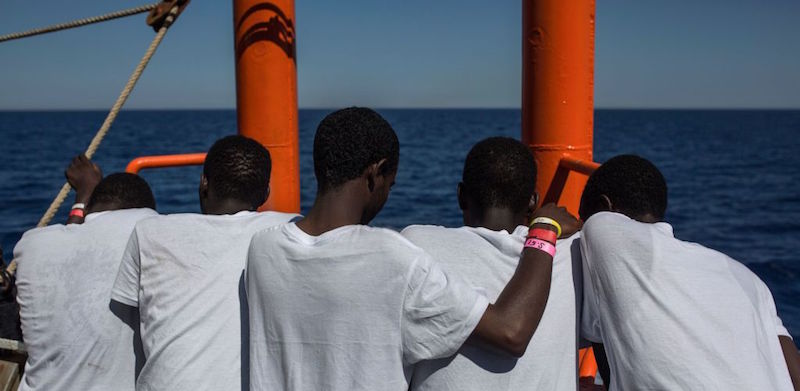
I matematici si divertono con poco.
![Congetture piuttosto inutili [Pillole]](https://www.ilpost.it/wp-content/uploads/2019/10/ilpost-anteprima-colore.png)
Sono arrivati i computer, e si è scoperto di avere bisogno dei numeri casuali. Come ottenerli?

Qualche rapida informazione sui generatori di numeri pseudocasuali

Nulla di particolare, a prima vista: un problemino stupido. Peccato che sia uno scherzo [Continua...]
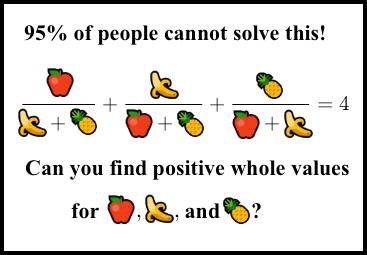
Perché il metodo per moltiplicare con le dita due numeri tra 6 e 9 funziona? [Continua]

È impossibile dare un nome a (quasi tutti) i numeri trascendenti. Pi greco ed e sono insomma un'eccezione. [Continua]

Nessuno sa se i numeri di Lychrel esistano davvero, almeno in base 10. Però se ne può lo stesso parlare.

Alcuni numeri sono più interessanti di altri, almeno per chi ama cercare le loro proprietà strane.

La differenza tra inglese britannico e statunitense si riflette persino nei numeri: quando si sente parlare di “bilione” occorre fare molta attenzione!

Non è semplice scegliere numeri a caso! Ecco un esempio di qualcosa che non funziona.

Noi esseri umani non siamo bravi con i numeri casuali. Voi come fareste?

![Un giorno perfetto [Pillole]](https://www.ilpost.it/wp-content/uploads/2019/10/ilpost-anteprima-colore.png)
Il grande matematico francese congetturò che tutti i numeri di una certa atruttura fossero primi. Si era sbagliato, e di grosso!

Pensavate che con i numeri immaginari avessimo finito le possibilità di creare numeri? Mannò, si può ancora andare avanti! L'unico guaio è che bisogna rassegnarsi a cedere qualcosa...

Un problema classico che può essere risolto con un metodo automatico.
