Come sette ponti portarono a una nuova matematica
Cominciò tutto a Königsberg quasi tre secoli fa con un problema irrisolvibile, che stimolò l'immaginazione di Eulero
di Emanuele Menietti
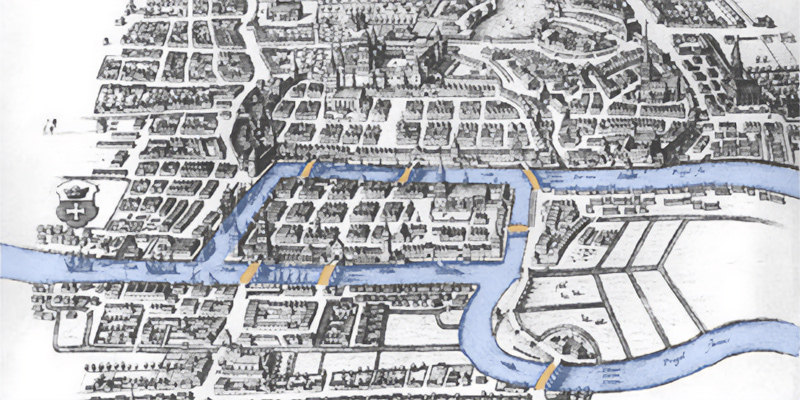
Nell’antica città prussiana di Königsberg, oggi l’exclave russa Kaliningrad, c’erano sette ponti che collegavano la terraferma e due grandi isole, circondate dal fiume Pregel. Si racconta che circa tre secoli fa gli abitanti della zona avessero tra i loro passatempi quello di provare ad attraversarli tutti e sette uno di fila all’altro, senza però percorrere lo stesso per due volte, ma che nessuno ci riuscisse mai veramente. Erano i primi sperimentatori inconsapevoli di un problema che avrebbe portato allo sviluppo di una nuova forma di matematica, e che avrebbe coinvolto uno dei più grandi matematici di tutti i tempi: Eulero.
A dirla tutta non ci sono molti elementi storici per confermare che l’impresa fosse una fissazione degli abitanti della città. Di sicuro la faccenda dei ponti di Königsberg aveva appassionato Carl Gottlieb Ehler, un matematico che sarebbe poi diventato sindaco di una città vicina. Dopo essersi a lungo scervellato sul problema entrò in contatto tramite un amico con Eulero, e gli scrisse per porgli il problema dei sette ponti. Voleva capire se davvero non ci fosse soluzione e quale fosse la spiegazione matematica, tale da poter essere applicata anche in altri contesti.
Inizialmente Eulero pensò che la richiesta non avesse nulla a che fare con la matematica e non le diede molto seguito. I problemi irrisolti o irrisolvibili esercitano però una certa fascinazione tra i matematici, di conseguenza Eulero non lasciò completamente perdere la storia di Königsberg, finendo infine per appassionarsi al problema. Osservò una mappa della città con i ponti che mettevano in comunicazione le due isole con la terraferma e un ponte che consentiva di passare anche da un’isola all’altra, chiedendosi quale fosse l’approccio migliore da seguire per venirne a capo. Sapeva che doveva semplificare il più possibile il problema, eliminando le distrazioni.
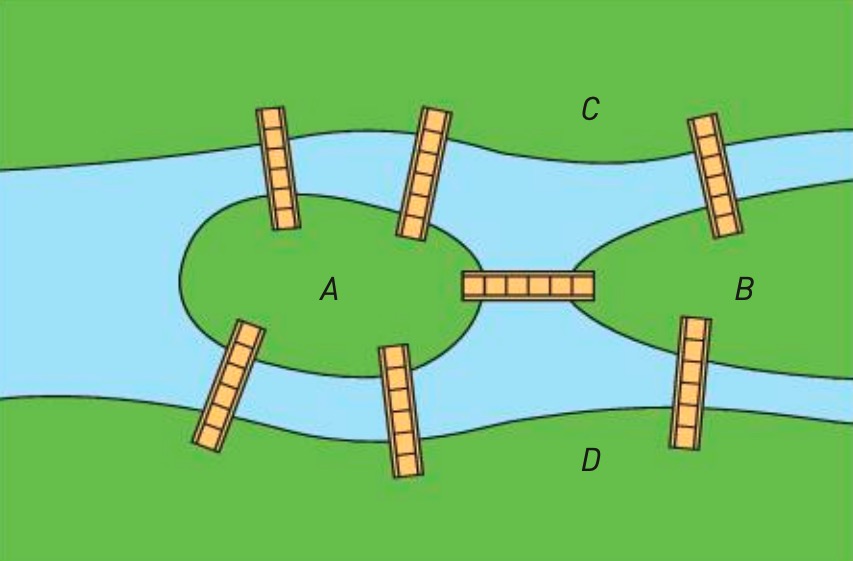
(Zanichelli)
Come prima cosa notò che il percorso seguito su ogni pezzo di terra era sostanzialmente irrilevante, perché ciò che contava era semplicemente la sequenza con cui venivano attraversati i sette ponti. Semplificò quindi il problema rendendolo in termini più astratti, usando i punti per i pezzi di terra e linee a simboleggiare ciò che li univa.
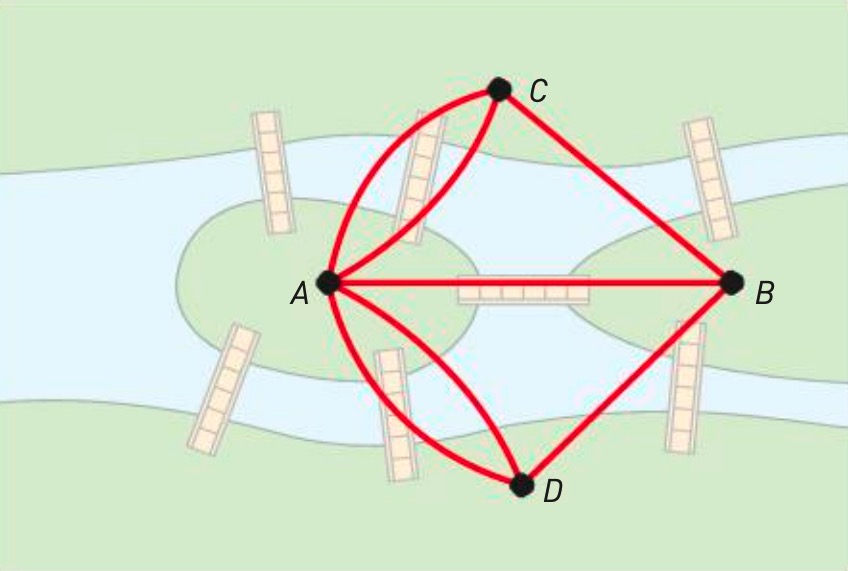
(Zanichelli)
Con quella semplificazione, Eulero aveva posto le basi per quella che oggi chiamiamo teoria dei grafi, fondamentale in numerosi ambiti – dalla matematica all’informatica – per schematizzare i processi e le soluzioni e dare loro un “senso” matematico. In termini più attuali, possiamo dire che Eulero identificò nei pezzi di terra quelli che nella teoria dei grafi si chiamano “nodi” (o “vertici”) e nei ponti quelli che nella stessa teoria sono detti “archi”.
La nuova rappresentazione di Eulero poteva essere valida per molti altri ambiti, non solo per le vie e i ponti di Königsberg. Lo schema mostrava infatti che solamente le informazioni legate al modo in cui erano collegati i nodi era importante, mentre la forma complessiva del grafo e il modo in cui era rappresentato erano secondari. In altre parole, dipendeva tutto dai nodi e dagli archi che li mettevano in comunicazione.
Ottenuto un nuovo modo di rappresentare il problema, Eulero provò a capire la questione dell’unico attraversamento di tutti e sette i ponti partendo da alcune considerazioni generali. Notò che fatta eccezione per i punti di partenza e arrivo, quando si raggiunge un nodo tramite un ponte lo si può poi abbandonare solo attraversando nuovamente un ponte. Detta più semplicemente, se raggiungi un’isola in mezzo a un fiume tramite un ponte, puoi abbandonare l’isola solo ripercorrendo lo stesso ponte (quindi lo percorri due volte). Se le regole del gioco sono di usare una sola volta un ponte, avrai bisogno di un altro ponte per lasciare l’isola (in questo caso percorri due ponti).
Ne consegue che il numero di volte in cui si raggiunge un nodo (che non sia all’inizio o alla fine del percorso) è uguale al numero di volte in cui lo si lascia: ponte – isola – ponte.
Se ogni ponte può essere attraversato una sola volta, allora il numero di ponti che collega ogni nodo eccetto quelli di partenza e di arrivo deve essere pari: metà consentono di raggiungerlo e metà di lasciarlo. Per intenderci, se un nodo fosse collegato da tre ponti, potrei arrivarci con il ponte 1, lo potrei poi abbandonare con il ponte 2 e tornarvi nuovamente col ponte 3, ma a quel punto per lasciare il nodo dovrei ripassare su un ponte già utilizzato non disponendo di un quarto ponte. Pessime notizie per Carl Gottlieb Ehler.
I quattro nodi della città erano infatti toccati da un numero dispari di ponti: uno era toccato da cinque ponti, mentre gli altri tre da tre ponti. Considerato che al massimo due nodi possono fare rispettivamente da punto di partenza e di arrivo, non c’è modo di fare una passeggiata attraversando una sola volta tutti e sette i ponti.
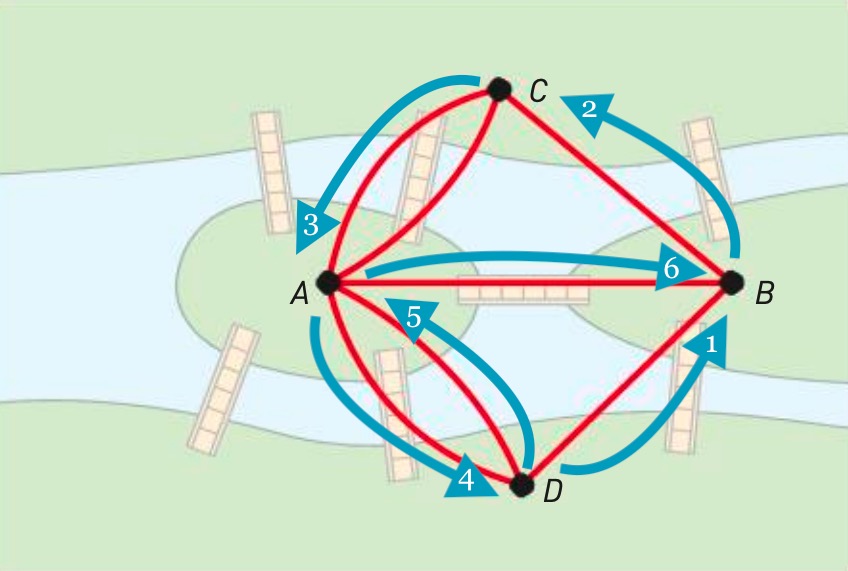
Il numero nella freccia indica l’ordine dei vari attraversamenti dei ponti
Usando i termini della teoria dei grafi, possiamo dire che la possibilità di attraversare una sola volta ogni arco in un grafo dipende dai “gradi” dei nodi. Il grado di un nodo indica semplicemente il numero di archi che lo toccano. Per esempio, il nodo “A” nell’immagine qui sopra è di grado 5.
Dai propri studi Eulero derivò una teoria, che oggi non a caso chiamiamo “cammino euleriano”, e che può essere applicata a tutti i grafi con almeno due nodi. Un cammino che tocchi tutti gli archi una sola volta è possibile solamente a una di queste due condizioni. La prima è che ci siano esattamente due nodi di grado dispari e i restanti di grado pari. In questo caso i punti di partenza e di arrivo sono i due nodi di grado dispari.
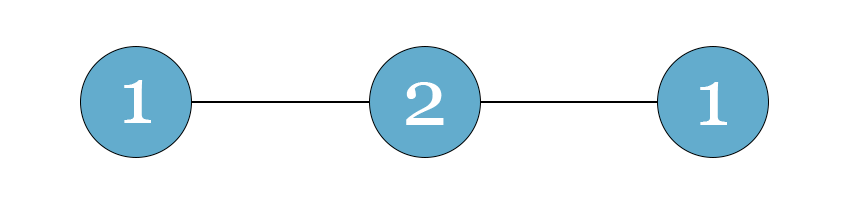
Cammino euleriano, il numero nel cerchio indica il grado
La seconda si verifica quando tutti i nodi sono di grado pari, cosa che consente di far coincidere il nodo di partenza con quello di arrivo, a prescindere da quello che viene scelto per primo. In questo caso il grafo viene definito un circuito euleriano.
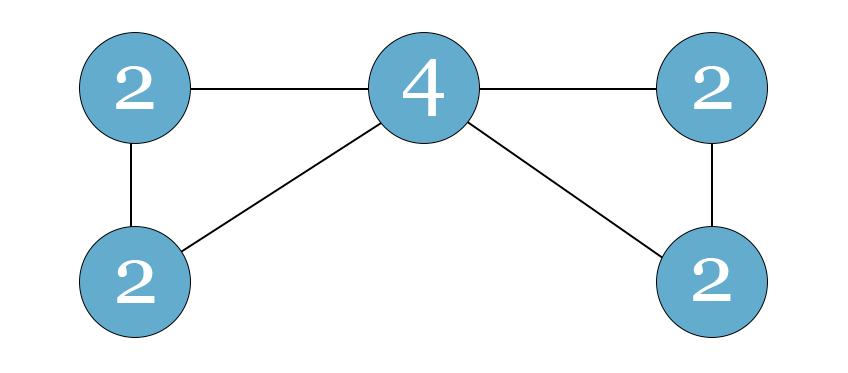
Circuito euleriano, il numero nel cerchio indica il grado
Tornando a Königsberg, l’unico modo per creare un cammino euleriano è fare a meno di uno qualsiasi dei sette ponti della città. E in effetti nel corso della Seconda guerra mondiale il problema fu risolto in modo piuttosto drastico, quando i bombardamenti sovietici distrussero ben due ponti cittadini. Durante la guerra andò distrutta buona parte della città, che fu poi ricostruita quando passò sotto il controllo dell’Unione Sovietica e in seguito della Russia con il nome di Kaliningrad.
Nonostante i traumatici sviluppi degli ultimi 80 anni, il precedente nome della città continua a essere ancora utilizzato ai giorni nostri, in parte grazie al proverbiale problema dei suoi ponti. Dimostrando l’impossibilità di attraversarli tutti una volta sola, Eulero mise le basi per la teoria dei grafi e per il successivo sviluppo della topologia, la parte della geometria che si occupa dello studio delle proprietà degli oggetti matematici, che non cambiano quando vengono deformati (a patto di non creare strappi, sovrapposizioni e incollature).



