La media dell’indeciso
Un modo interessante per calcolare una media sensata nel caso di valori molto distanti [Continua]
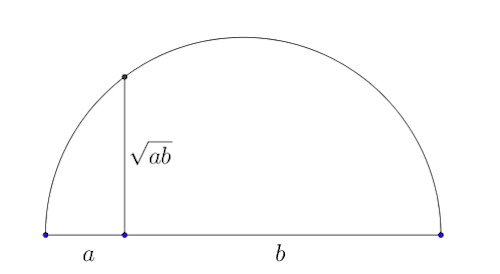
Un modo interessante per calcolare una media sensata nel caso di valori molto distanti [Continua]

La notazione matematica è fatta di convenzioni per semplificare la vita. Se la rendono più complicata, forse c'è qualcosa di sbagliato in partenza.

Un cortometraggio un po' surreale
![A comme Arithmétique [Pillole]](https://www.ilpost.it/wp-content/uploads/2019/10/ilpost-anteprima-colore.png)
No, non sto parlando della numerazione binaria, ma di una simpatica proprietà dei numeri [Continua]

![Ufficio Complicazioni Affari Semplici [Pillole]](https://www.ilpost.it/wp-content/uploads/2019/10/ilpost-anteprima-colore.png)
Non è vero che Euclide ha dimostrato che ci sono "infiniti" numeri primi, e non è nemmeno vero che ha fatto una dimostrazione per assurdo [Continua]

La maggior parte dei matematici non ha problemi ad accettare le dimostrazioni per assurdo. Ma c'è chi non è d'accordo; a costoro tocca però lavorare parecchio e inventarsi nuove idee.

Non è che i matematici predichino bene e razzolino male: il punto è che loro sono inconsciamente abituati a distinguere la scoperta di una proprietà dalla sua dimostrazione, ma si dimenticano di mostrare il momento della scoperta.

come ottenere i numeri da 1 a 100 in modi creativi
![Integermania [Pillole]](https://www.ilpost.it/wp-content/uploads/2019/10/ilpost-anteprima-colore.png)
Con un po' di contorsioni, e ammettendo l'esistenza a priori di 0 e 1, è possibile definire una singola operazione dalla quale si possono ottenere le quattro usuali operazioni.

Certi numeri, come e oppure π, appaiono davvero ovunque!
![Numeri che appaiono in posti impensati [Pillole]](https://www.ilpost.it/wp-content/uploads/2019/10/ilpost-anteprima-colore.png)
Gli Elementi non parlano solo di geometria, ma anche di aritmetica; e anche qua brilla l'esposizione di Euclide.

Non è affatto facile dividere equamente un pagamento a seconda del risultato di un gioco, soprattutto se i giocatori sono più di due!

Un algoritmo che forse non è così vecchio come dicono, ma è comunque interessante... almeno in teoria.

Perché mai il metodo di calcolo manuale della radice quadrata funziona?

una variante moderna di una successione ben nota. C'entra Conway, quindi è sicuramente interessante...

No, 0^0 non è una faccina con gli occhiali ma un'operazione matematica. Però non è che tutte le operazioni matematiche siano sensate...

Riuscire a dire qual è il giorno della settimana corrispondente a una data qualunque senza avere a disposizione un calendario sembrerebbe un compito impossibile; ma esistono tecniche mnemoniche alla portata di tutti.

I numeri di Fibonacci compaiono nei posti più inaspettati. Nulla di strano, perché la relazione che li genera è molto semplice; ma in ogni caso ci sono delle proprietà simpatiche.

Due giochi della serie "prendi i gettoni" dalle caratteristiche a prima vista simili; ma mentre per il Nim è facile trovare una strategia vincente il gioco di Whytoff è un po' più ostico.
