Non usate a sproposito la legge di Benford
D’accordo, Donald Trump ha un modo molto personale di vedere le cose. Ma ci sono molte altre persone che sono convinte che ci siano in effetti stati dei brogli, e per dimostrarlo usano la matematica. In questo post su StackExchange vengono mostrati due esempi di come ci sia qualcosa di strano, in entrambi i casi usando la legge di Benford. (Ne avevo parlato sul Post anni orsono; sennò trovate anche qualcosa sul mio sito).
Per chi non avesse voglia di spulciare i miei vecchi documenti, la legge di Benford afferma che prendendo una quantità sufficientemente grande di valori, dal numero di abitanti delle municipalità alla quantità di metalli estratti nelle varie nazioni, la prima cifra di questi valori non avrà una distribuzione più o meno costante, ma la cifra iniziale 1 capiterà all’incirca il 30% dei casi, la cifra 2 nel 17,6% dei casi e via via a scalare fino al 9 che apparirà nel 4,6% dei casi. C’è anche una legge di Benford sulla seconda cifra, anche se lì le differenze sono minori.
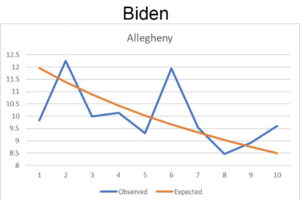
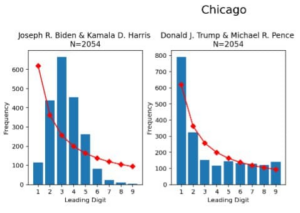
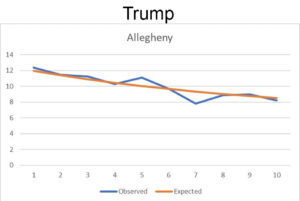Nel post suindicato venivano mostrate le distribuzioni della prima cifra dei voti a Biden e a Trump a Chicago, che danno i risultati mostrati qui a sinistra; più in basso vedete invece la frequenza della seconda cifra in una specifica contea. In entrambi i casi è anche indicata la frequenza che ci si aspetterebbe secondo la legge di Benford. I brogli sono evidenti, nevvero? Non è possibile che in un caso ci siano così tanti scostamenti e nell’altro no!
