Quizzini per Natale 2018
Che Natale sarebbe senza i quizzini del Post? Le risposte tra una settimana. Gli ultimi due sono più difficili, magari poi posterò un aiutino 😉
1. Non essere ottusi
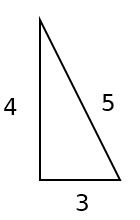
Considerate tutti gli insiemi I di cento numeri interi positivi distinti con la seguente proprietà: dati tre qualunque elementi a, b e c in I, il triangolo di lati a, b, c non è mai ottusangolo. Se S(I) è la somma dei perimetri di tutti i possibili triangoli diversi formati da tre elementi (non necessriamente distinti) di I, qual è il suo valore minimo?
(Se gli elementi di I fossero {100, 101, … 199} un triangolo di lati 100, 100, 100 è da contare, così come uno di lati 100, 100, 101)
2. Un primo di mezzo
Sia p un numero primo. Trovate le soluzioni (relative a p) intere (positive, negative o nulle) dell’equazione p(x+y)=xy. (Ricordo che 1 non è un numero primo, e tantomeno lo è 0)
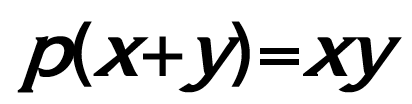
3. Massimo comun divisore
I numeri naturali a e b sono tali per cui ((a+1)/b)+((b+1)/a) è intero. Se d è il massimo comun divisore tra a e b, dimostrate che d ≤ √(a+b).
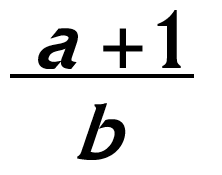
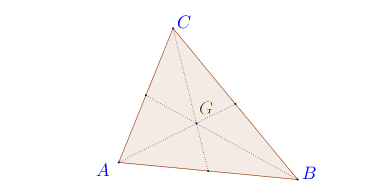
4. Baricentro
Sia G il baricentro del triangolo ABC. Dimostrate che se AB + GC = AC + GB allora il triangolo è isoscele.
5. Spioni
Nell’isola di Spiolandia ci sono 16 agenti segreti. Ciascuno di essi spia almeno uno dei suoi colleghi; se poi un agente A spia un agente B, allora l’agente B non spia l’agente A. Inoltre dato un qualunque insieme di dieci agenti A1, A2, A3, …, A10, è possibile ordinarli in una catena in modo che il primo spii il secondo, il secondo il terzo, e così via, fino al decimo che spia il primo. Dimostrate che allora esiste una catena simile anche con 11 agenti qualunque.