Problemini per Pasqua 2015
Stavolta i problemini sono tratti da varie gare matematiche (per giovani, non preoccupatevi…) e recuperati dal sito Gifted Mathematics.
1. Non troppa area
All’interno (quindi non sul perimetro!) di un quadrato di lato 1 ci sono nove punti. Dimostrare che se ne possono trovare tre che formano un triangolo di area minore di 1/8. Ovviamente tre punti collineari formano un triangolo di area 0.
2. Radici, solo radici
Calcolate il valore (ammesso che sia finito…) dell’espressione qui sotto.
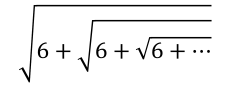
3. Prodotti notevoli
A parte la soluzione banale (0,0), quante altre soluzioni intere (positive o negative) ci sono per la seguente equazione?
(m2+n)(m+n2) = (m+n)3
4. Cancellazioni
Vi viene detto che in una delle soluzioni dell’equazione
x1x2 + x2x3 + x3x4 + … + xnx1 = 0 tutti gli xi hanno valore +1 oppure −1. Dimostrate che n dev’essere multiplo di 4.
5. Zigzag
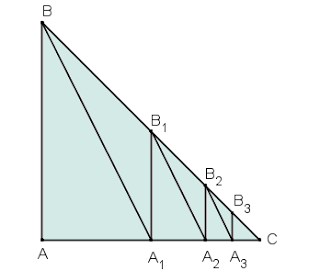Il triangolo ABC qui a fianco ha i cateti lunghi 4. Il punto A1 è a metà del segmento AC e il segmento A1B1 è perpendicolare ad AC; similmente il punto A2 è a metà del segmento A1C e il segmento A2B2 è perpendicolare ad A1C, e così via all’infinito. Quanto vale la somma di tutti i segmenti BA1+B1A2+B2A3+…?
