Problemini per Pasqua 2021
Come già successo in passato, i problemi sono tratti dal libro di Hugo Steinhaus One Hundred Problems in Elementary Mathematics (numeri 41, 44, 51, 69, 71). Tra una settimana le soluzioni.
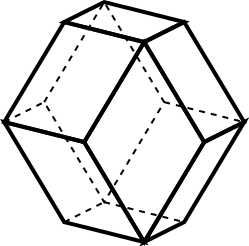
1. Rombododecaedro
Una formica si trova su un vertice di un rombododecaedro – un solido semiregolare formato da 12 rombi, come si vede nella figura qui sotto – e vuole fare un percorso attraverso i suoi spigoli in modo da toccare una sola volta tutti i vertici e tornare al punto di partenza: in matematica si parla di ciclo hamiltoniano. Può riuscire nel suo intento?
2. Lavorare in 3D
La superficie di un cubo è formato da sei quadrilateri (per la precisione, quadrati) uguali. È possibile costruire un solido concavo la cui superficie sia formata da un certo numero di quadrilateri tutti uguali tra di loro?
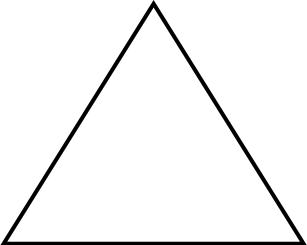
3. La torta triangolare
Gino e Pino devono dividersi una torta a forma di triangolo equilatero. Pino propone di prendersi una fetta che otterrà facendo un unico taglio per dividere la torta, e Gino acconsente, chiedendo però di scegliere lui per quale punto il taglio debba passare. Sapendo che Pino vuole prendersi la maggior parte della torta, quale punto conviene che Gino scelga? Naturalmente potete assumere la torta perfettamente uniforme.
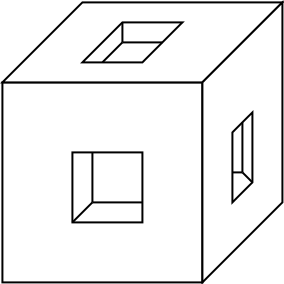
4. Divisioni primarie
Immaginate di avere una pianta del catasto con un appezzamento rettangolare diviso in due parti sempre rettangolari, come nella parte superiore della figura. È ovvio che la divisione è stata fatta in un unico passo. In una divisione in tre parti come quella nella parte inferiore della figura, invece, non è possibile decidere se la divisione è stata fatta in un unico momento, oppure prima è stata fatta la divisione in verticale e in un tempo successivo quella in orizzontale. Chiamiamo divisione primaria quella del primo tipo e divisione secondaria quella del secondo tipo. Naturalmente è sempre possibile avere divisioni secondarie con un numero qualunque di parti; basta fare tante strisce verticali. Non è invece possibile avere divisioni primarie in 3, 4 e 6 parti. Sapete costruirne una in 5 parti?

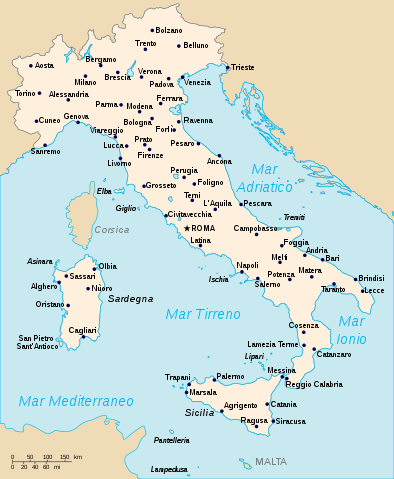
5. Distanze
Prendete una cartina dell’Italia e disegnate un segmento che unisca ciascuno dei capoluoghi di provincia con quello più vicino. (Supponete che sia sempre possibile stabilire quale sia quello più vicino: non ci siano insomma due città alla stessa distanza). Dimostrate che non è possibile che ci sia una città connessa ad altre sei città.