Svaligiare la banca

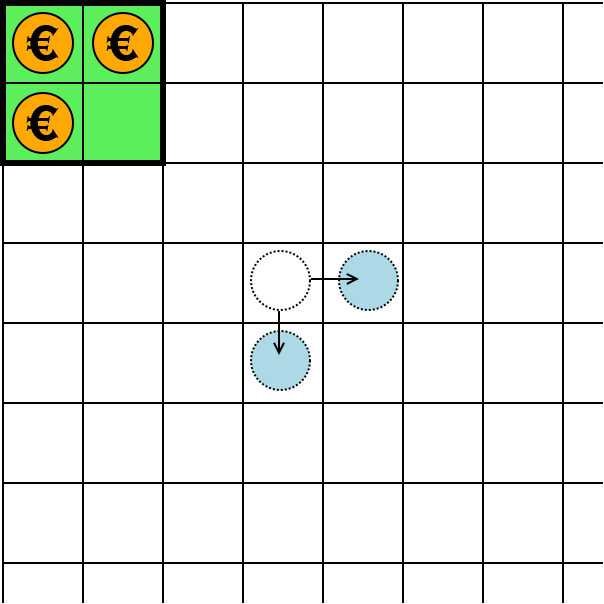
Un paio di settimane fa Alex Bellos ha presentato nella sua rubrica sul Guardian questo problema matematico. Abbiamo una “banca matematica”, come mostrato nella figura qui sotto: un quadrato due per due all’angolo di un infinito quadrante. Come vedete, la banca contiene al suo interno tre monete. Una moneta in una qualunque posizione può essere tolta se la posizione a destra e quella sotto di essa sono entrambe libere: in tal caso esse verranno automaticamente riempite con due nuove monete. Le monete tratteggiate nella figura spiegano cosa succede: quella bianca viene tolta, quelle azzurre aggiunte. Si direbbe che con la creazione di danaro dal nulla si può diventare ricchi, ma come sempre c’è un codicillo: si possono prendere tutte le monete presenti nello schema solo se la banca non ne contiene più nessuna. Come si può riuscire nell’intento? Pensateci un po’ su.

(altro…)