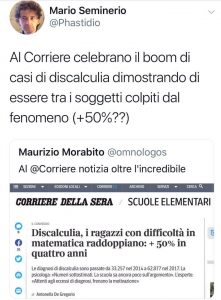
Ah, la discalculia!
Rubo l’immagine dalla coppia Morabito-Seminerio per fare qualche considerazione sulle capacità del titolista, in questo caso del Corriere della Sera (ah, la parte finale del titolo è stata eliminata, ora recita solo «Discalculia, i ragazzi con difficoltà in matematica raddoppiano»). A parte le battute banali, abbiamo due errori matematici che sono molto comuni, e per cui quindi vale la pena di spendere un paio di parole in più.
Siamo tutti d’accordo che passare da 33.257 a 62.877 significa quasi raddoppiare, e direi che possiamo accettare la semplificazione spannometrica “raddoppiati”. Da dove arriva il +50%, allora? La mia ipotesi è che qualcuno abbia fatto il conto alla rovescia. Se da 100 si passa a 200, abbiamo raddoppiato il numero iniziale: però passando da 200 a 100 siamo scesi solo del 50%. Se uno non è bravo in matematica, può pensare che il 50% funzioni in entrambe le direzioni, come succederebbe se sommassimo anziché moltiplicare: ma questo non è il caso, come vi siete certo accorti. Attenzione che casi come questo sono molto comuni! Se io aumento un prezzo di un prodotto del 20% e poi ti faccio uno sconto del 20% non vado in pareggio ma in perdita. Di nuovo, qualche conto ci può aiutare: da 100 si passa a 120, e il 20% di 120 è 24, che tolti da 120 ci portano a 96.
Non so in quanti abbiano notato il secondo errore: dal 2014 al 2017 gli anni sono tre e non quattro. Questo invece potrebbe essere il risultato di un fencepost error, errore della staccionata. Questo tipo di errore capita spesso con i bambini piccoli che non sanno fare le sottrazioni ma contano ancora con le dita. Per arrivare da 2014 a 2017 si conta 2014, 2015, 2016 e 2017: i numeri sono quattro, perché contiamo anche quello di partenza che sarebbe invece il valore “zero” e quindi non si conta. L’errore si chiama così perché per fare una staccionata lunga 10 metri distanziando i pali di un metro ce ne vogliono 11 e non 10: in questo caso il punto zero serve eccome!