Ausilii per le moltiplicazioni
Adesso va di moda la moltiplicazione alla giapponese, quella con i video che mostrano le righe che si incrociano e per cui basta contare gli incroci per trovare la soluzione. Sarà. Magari vi siete accorti anche voi che negli esempi si moltiplica sempre 123×321 e non 789×987, perché altrimenti ci si sbaglierebbe a contare i puntini. Non ditelo troppo in giro, ma la moltiplicazione giapponese non è poi tanto diversa da quella che abbiamo imparato a scuola: a parte la disposizione dei numeri sotto forma di righe, l’unica vera differenza è che nei vari prodotti parziali dobbiamo mettere subito i riporti, mentre qui li si lascia tranquilli fino alla fine e soprattutto che non dobbiamo imparare a memoriale tabelline, impresa che può risultare ostica anche per molti scolari: figuriamoci qualche secolo fa. Come si faceva però alcuni secoli fa a fare le moltiplicazioni, a parte mettersi con calma a scrivere sulla carta tutti i passaggi?
bastoncini di Nepero (da https://en.wikipedia.org/wiki/File:Bones_of_Napier_%28board_and_rods%29.png )
La prima soluzione davvero pratica a questo problema fu ideata da Nepero, quello che aveva anche inventato i logaritmi. I cosiddetti bastoncini di Nepero – ma in inglese il nome è molto più evocativo: Napier’s bones, le ossa di Nepero – non sono altro che le tabelline scritte su un listello di legno o di metallo, con i numeri delle unità e delle decine separate da una barra diagonale, come nel disegno qui a fianco. Nepero spiega l’uso dei suoi bastoncini nella sua opera del 1617 Rhabdologiae seu Numerationis per virgulas libri duo (se volete, potete scaricarvela da archive.org…) Per moltiplicare un numero di più cifre per uno di una sola cifra si mettevano l’uno vicino all’altro i bastoncini corrispondenti alle cifre del moltiplicatore, e si sommavano i due triangoli con un cateto in comune: la cifra del regolo di destra è infatti il riporto. Insomma, un utile ausilio meccanico, che ebbe un meritato successo almeno fino a tutto l’Ottocento.
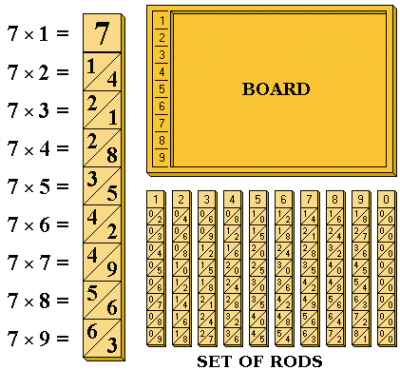
Ma quelli che vale davvero la pena di vedere all’opera sono i regoli di Genaille-Lucas, ideati nel 1891 dall’ingegnere ferroviario francese Henri Genaille su idea del grande matematico ricreativo Édouard Lucas. Qual è il maggiore problema dei bastoncini di Nepero? Bisogna comunque sommare i riporti, come ho spiegato sopra. Genaille ebbe l’idea geniale (“genialle?”) di indicare il valore corrispondente al riporto in modo grafico. I suoi regoli sono mostrati nella figura qui a destra.

regoli di Genaille-Lucas ( da https://it.wikipedia.org/wiki/File:Genaille-Lucas_rulers_full_600.png )
Come vedete, ciascun regolo è diviso in due parti: quella di destra contiene tutti i risultati possibili per il prodotto tra il numero sul regolo e quello dell’indice, considerati anche tutti i riporti possibili dalla cifra precedente. Prendiamo per esempio il regolo numero 7 e guardiamo come è fatta la sezione corrispondente all’indice 4. Il numero più in alto è un 8, e in effetti 7×4=28; poiché il riporto possibile da un prodotto precedente (sempre per quattro…) può essere al massimo 3, sotto l’8 vengono scritte altre tre cifre. Il triangolo, oppure come in questo caso i due triangoli, disegnato a sinistra sono un modo grafico per indicare qual è il riporto: in questo caso se il risultato è 8 oppure 9 il riporto è 2, e quindi la punta del triangolo corrisponderà alla terza riga del regolo successivo (la prima riga sarebbe un riporto zero…); se il risultato è 0 oppure 1, la punta del triangolo corrisponderà alla riga inferiore perché il riporto è 3. Il risultato di una moltiplicazione si legge muovendosi da una punta all’altra dei triangoli e trascrivendo le cifre man mano che si incontrano: non è così più necessario imparare la tavola pitagorica né fare le somme, per la gioia di tanti studenti.
Certo, ormai anche i regoli di Genaille sono caduti nel dimenticatoio, resi inutili dall’elettronica: ma volete mettere la bellezza intrinseca?



