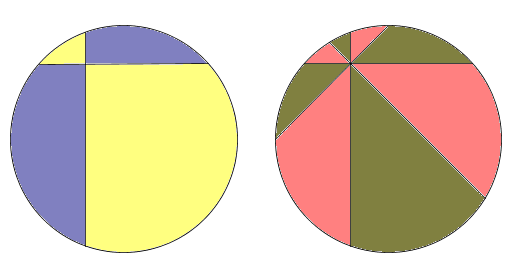Il teorema della pizza
Aldo ed Ester hanno preso una pizza e se la devono dividere. Aldo fa due tagli perpendicolari che però non passano per il centro della pizza, e poi fa per prendere la fetta maggiore (come nell’immagine a sinistra qui sotto). Ester lo guarda male, e allora Aldo dice “Hai ragione. Facciamo così: prendo quella insieme alla la fetta più piccola e tu quelle di mezzo, così siamo pari”. Ester lo ferma, gli prende il coltello e fa altri due tagli, che passano sempre per lo stesso punto e bisecano le fette: ora ci sono otto fette, tutte con un angolo di 45 gradi. Sorride poi al compagno, e gli dice soavemente: “Ora va molto meglio. Io prendo la fetta più grande, e poi andiamo avanti in senso orario, prendendo ciascuno la fetta successiva”. Allo sguardo perplesso di Aldo, continua: “O se preferisci la fetta grande la prendi tu, e poi proseguiamo come ho detto. Scegli pure, ma fa’ in fretta che la pizza si raffredda.” Che cosa consigliate ad Aldo di fare, a parte imparare a tagliare la pizza passando dal centro?
Un taglio in quattro parti e un altro taglio in otto parti
