Il paradosso di Braess
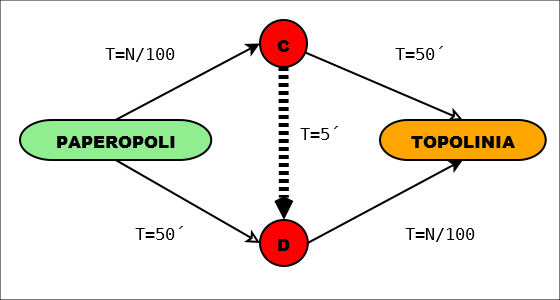
Come certo saprete tutti, ci sono due strade diverse per andare da Paperopoli a Topolinia: una passa per Catsville e l’altra per Dogsburg. Ogni mattina ci sono ben 4000 persone che prendono l’auto per andare da una città all’altra; mentre i tratti Catsville-Topolinia e Paperopoli-Dogsburg sono abbastanza ampi perché il tempo di percorrenza sia sempre di 50 minuti, gli altri due tratti sono intasati, e percorrere ciascuno di essi richiede N/100 minuti, dove N è il numero di auto che impegna il tratto di strada. Ciascun automobilista sceglie naturalmente il percorso che per lui è il più veloce: alla fine la situazione si è stabilizzata, e i paperopolesi si dividono esattamente a metà, 2000 per strada. Il tempo complessivo per il viaggio è quindi di 2000/100 + 50 = 70 minuti per tutti.
Catsville e Dogsburg sono però molto vicine, e così Filo Sganga ha convinto i sindaci delle due città a costruire una nuova strada che le unisca direttamente. Il tempo di percorrenza della nuova strada sarà di soli 5 minuti. Zio Paperone avrebbe voluto costruire lui la strada: ma scoprendo che la commissione era presieduta da Brigitta scappò a gambe levate, e l’appalto fu vinto da Rockerduck. Secondo voi, cosa è successo dopo che la strada è stata completata?