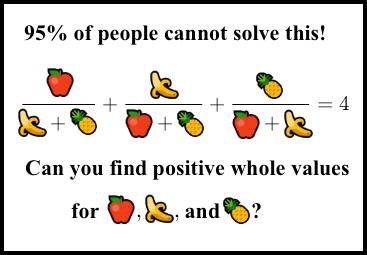Un quizzino non proprio così facile
- Condividi
- X
- Regala il Post
Paolo Marino mi segnala un articolo di Quora che tratta uno di quei memi che ogni tanto si vedono nelle nostre bacheche Facebook. Ecco la figura in questione:
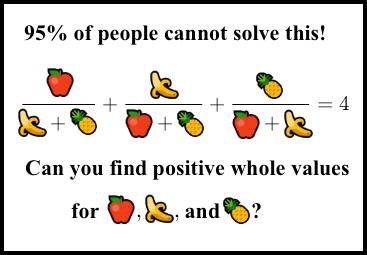
Tag: teoria dei numeri
Consigliati
Perché gli atleti italiani sono “azzurri”?
È per via di uno dei colori della famiglia reale Savoia, in uso da molto prima della bandiera tricolore italiana
Sapete cos’è la kava?
Una sostanza con effetti ansiolitici che negli Stati Uniti va di moda e viene bevuta al posto dell'alcol, ma che potrebbe avere effetti tossici
In Spagna e America Latina c’è grande scandalo per queste persone
Da settimane si parla molto dei "therians", una piccola sottocultura presa pretestuosamente di mira per criticare le derive delle politiche progressiste