La scala del diavolo
Quando verso la metà del diciannovesimo secolo iniziò la grande opera di consolidamento dell’analisi matematica, la spinta non fu certo data dai professori che volevano tendere tranelli ai propri studenti: molto più banalmente ci si era accorti che alcune idee “ingenue” che si avevano sul comportamento delle funzioni andavano benissimo quando si dovevano trattare enti fisici (da cui la famigerata definizione di “well behaved functions”, cioè “funzioni su cui si possono applicare i teoremi che ci interessano”) non erano sempre vere, e quindi bisognava fermarsi e capire cosa stava succedendo. Un esempio tipico di queste funzioni, che inizialmente furono chiamate patologiche perché si pensava fossero eccezioni e non la norma, è la funzione di Dirichlet: χ(x) vale 0 se x è un numero irrazionale e 1 se x è razionale. Il grafico di questa funzione, se di grafico si può parlare, assomiglia a due rette orizzontali un po’ sbiadite perché mancano loro infiniti punti: quella più in alto dovrebbe essere più sbiadita perché ha meno punti, ma non credo se ne accorgerebbe nessuno. Ma ci sono funzioni molto più curiose!

I primi passi della costruzione dell’insieme di Cantor (da Wikipedia)
Prima di presentarvi la funzione, però, credo sia utile ripassare come è composto l’insieme di Cantor, di cui molti di voi probabilmente hanno sentito parlare. Esso è un sottoinsieme del segmento [0,1], che può essere costruito solo con un numero infinito di operazioni. Al primo passo si divide il segmento in tre parti uguali e si butta via quella di mezzo (lasciando i due estremi, ma in realtà il risultato finale cambia poco). Al secondo passo si toglie il terzo centrale dai due segmenti rimasti; al terzo passo si toglie il terzo centrale dai quattro segmentini rimasti; e si continua così all’infinito. Il disegno qui a fianco mostra i primi passi della costruzione. Cosa rimane alla fine di tutto questo lavoro di eliminazione? L’insieme di Cantor, appunto. Approssimato molto bene dalla polvere che continua ad accumularsi sul mio pianoforte, l’insieme di Cantor contiene un’infinità (non numerabile, addirittura!) di punti, ovviamente tutti separati tra di loro. Attenzione: è possibile indicare un procedimento che, dato un numero, permette di stabilire se il punto corrispondente appartiene o no alla polvere di Cantor. Prendiamo il numero e scriviamolo in base tre: se la sua rappresentazione contiene solo le cifre 0 e 2 allora sta nell’insieme, mentre se c’è anche solo un 1 non ci sta. Tra l’altro, ecco perché nella costruzione ho lasciato entrambi gli estremi dei segmenti: sfrutto il fatto che i punti agli estremi dei segmenti da togliere hanno due possibili rappresentazioni, e quindi posso scegliere per gli estremi del primo segmento centrale le rappresentazioni 0,022222…3 e 0,200000…3 anziché 0,10000…3 e 0,111111…3
Ma quanto è lungo – o meglio, come dicono i matematici, qual è la misura dell’insieme di Cantor? Per essere più precisi bisogna prima chiedersi se una misura ce l’ha. Chi ha studiato analisi matematica sa che non è detto che un insieme qualunque sia misurabile: è il trucco alla base del paradosso di Banach-Tarski, quello che raddoppia le palle. In questo caso però il compito è facile. Al primo passo togliamo infatti un segmento di lunghezza 1/3: al secondo passo due segmenti di lunghezza 1/9, cioè un totale di 2/32; al terzo passo quattro segmenti di lunghezza 1/27, cioè un totale di 22/33. Se fate la somma di questi infiniti pezzi, cosa che non è difficile da fare visto che è una semplice serie geometrica, otteniamo 1; pertanto quello che rimane è di misura 0. Un vera e propria polvere, che però non possiamo nascondere sotto il tappeto!
Bene: abbiamo ora tutto l’armamentario per studiare la scala del diavolo. La funzione è definita nell’intervallo [0,1] e ha valori in [0,1]. La sua costruzione formale è definita così: dato un punto x,
- Scriviamo x in base 3.
- Se nello sviluppo di x troviamo un 1, sostituiamo tutte le cifre a destra del primo 1 con degli 0.
- Sostituiamo tutte le cifre 2 con degli 1.
- Leggiamo il numero (che ormai ha sole cifre 0 e 1) come se fosse scritto in base 2.
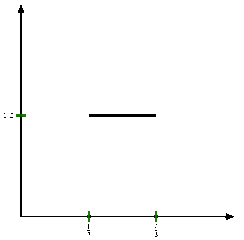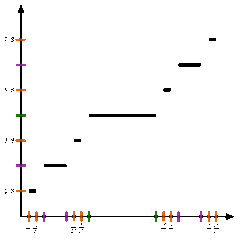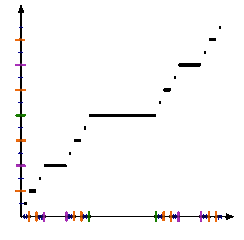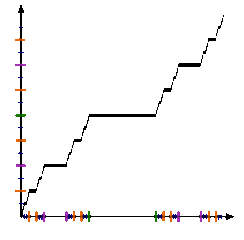
I primi passi per costruire la funzione di Cantor (da Wikipedia)
Chiaro, vero? Sì, sto scherzando. Leggendo così non si capisce molto. Forse è un po’ più chiara la GIF animata qui a fianco, presa da Wikipedia; provo comunque a far vedere cosa succede nei primi passi di un processo ricorsivo. Scrivendo i numeri in base 3, quelli da 0 a 1/3 escluso sono della forma 0,0…, quelli tra 1/3 e 2/3 escluso della forma 0,1…, quelli da 2/3 a 1 sono della forma 0,2… I valori del secondo gruppo vengono trasformati in 0,1, che letto come numero binario equivale a 0,5, e non si schiodano più; quelli del terzo gruppo alla fine saranno della forma 0,1…; quelli del primo gruppo per il momento restano identici. Prendiamo ora la seconda cifra decimale. Come nel caso precedente, i valori tra 1/9 e 2/9, che scritti in base 3 sono della forma 0,01…, diventano 0,01 in base 2, cioè 0,25; quelli da 7/9 a 8/9, della forma 0,21… diventano prima 0,21 e poi 0,11, che tradotto in base 10 è 0,75. Quelli da 2/9 a 1/3 diventano della forma 0,01…, quelli da 2/3 a 7/9 diventano della forma 0,10… e quelli da 8/9 a 1 diventano della forma 0,11… Andando avanti così, ogni pezzetto centrale di dimensioni 1/3 ha un valore che si trova a metà strada tra i due precedenti e alla fine si ottiene quella specie di scala che vedete in cima al post.
Alla fine abbiamo una funzione che sembra un po’ strana con quei pezzi in cui non si muove, ma in fin dei conti neanche poi troppo strana. Essa vale 0 per x=0, vale 1 per x=1, tocca tutti i valori tra 0 e 1, è non decrescente ed è continua, anzi uniformemente continua: nella definizione tipica di continuità con delta ed epsilon, il delta dipende solo da epsilon e non anche dal punto di partenza. Insomma, una funzione che sembra comportarsi bene. Peccato che non si sappia mai quando cresca! Nei punti in cui è piatta, la derivata è ovviamente zero; in quelli in cui non lo è, che corrispondono ai punti dell’insieme di Cantor, la derivata non è definita. Questo tra l’altro significa che l’integrale della derivata della funzione è una costante, e quindi non è la funzione stessa a meno di una costante: di nuovo, un risultato che per chi ha studiato al liceo è assolutamente incredibile. Direi che il nome “scala del diavolo” è più che appropriato, non credete?
Post scriptum: mentre cercavo informazioni sulla scala del diavolo ho scoperto che ne esiste anche una versione più “smussata”: la funzione punto interrogativo di Minkowski, ?(x). Il senso dell’umorismo dei matematici è terribile.
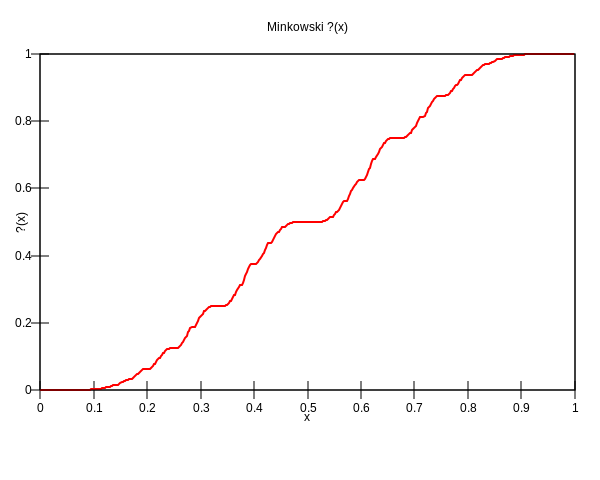
Funzione punto interrogativo di Minkowski (da Wikipedia)



